離散微分幾何学を用いた曲面のモデル化と生成|大崎純
1.はじめに
建築の大空間を覆う(包む)屋根構造には,古典的には球形シェルや円筒シェルなどの数式で表現できる幾何学的形状が用いられてきた。これらの曲面は円や直線などの簡単な数式の組み合わせで表現できるが,複雑な数式を用いると,さまざまな形状の曲面を生成できる。文献1(38章, 752ページで構成される)には,数式で表現できる線織面,回転体曲面,推動曲面,螺旋曲面,周期的曲面,極小曲面,ガウス曲率一定曲面などの多数の例が示されている。しかし,幾何学的形状(数式表現)だけでは曲面の形状は限定され,また,数式の係数をパラメータとして変更したときの形状の変化が直感的でなく,設計者の意図した形状を実現するのが困難である。このような問題点を解決するため,1990年代になって,CADで開発されたベジエ曲面,Bスプライン曲面,非一様有理Bスプライン曲面(non-uniform rational B-spline, NURBS)2-3などのパラメトリックな表現が建築曲面のデザインや最適化にも用いられるようになった。しかし,パラメトリック表現を用いても,表現できる形状はその基底関数の空間内であり,自由な形状を表現できるとはいえない。
一方,曲面を生成する際に,何らかの汎関数(エネルギー関数)を定めて,それを最適化手法を用いて最小化すると,全体と局所的な形状を自然に決定することができる。最も知られている例としては,与えられた境界を覆う曲面の面積を最小化することにより得られる極小曲面がある。この曲面は,平均曲率がいたるところで0であり,等張力の膜(石鹸膜)の釣合い曲面として建築の膜構造でも利用される。また,ガウス曲率がいたるところで0であるような曲面は可展面であり,平面から面内変形を与えることなく曲げ変形のみによって生成できる4。しかし,一般の曲面でのガウス曲率などの特性量の計算は極めて煩雑であり,NURBSなどのパラメトリック曲面を用いた場合でも,パラメータに関する高階の微分係数を必要とする5。さらに,これらの曲面を建築の屋根構造として用いるためには,曲面が得られた後で,三角形や四辺形のメッシュで曲面を分割し,有限要素解析によって力学的特性を評価する必要がある。
以上の理由により,曲面の生成から解析まで,一貫して同一の離散的なモデルを用いることができれば便利である。曲面の特性量を微分方程式を用いることなく差分や離散的な曲面(多面体)を用いて分析する研究分野を離散微分幾何学という6-8。2000年以降,離散微分幾何学を曲面形状生成に適用する研究がコンピュータグラフィックスや工業デザインの分野で活発に行われている9。本稿では,筆者が関わっているプロジェクト10の成果の一部として,汎関数の最小化によって定義される曲面を,離散微分幾何学の手法で求める例を紹介する11-12。
2.ガウス曲率流によるガウス曲率一定曲面の生成
極小曲面と可展面を一般化した曲面を線形ワインガルテン曲面(linear Weingarten surface, LWS)といい,曲面上の全ての点で平均曲率とガウス曲率の線形結合が一定である 13-14。 LWSは,次の汎関数Eを最小化することによって求められる。
![]()
ここで,Ηは平均曲率, Αは面積, Vは曲面が内包する空間の体積であり,α, β, γは 正の実数の定数である。
曲面の法線方向の変分(変化量)をψとし,最小化すべき汎関数の第一変分をψを用いて表現する。このとき ,停留条件としての Euler-Lagrange の方程式が満たされる方向(勾配と逆の方向)に曲面を変形することによって汎関数を最小化し,停留条件を満たす形状を求める方法を勾配流による方法といい,平均曲率 およびガウス曲率で表される勾配をそれぞれ平均曲率流¹⁵およびガウス曲率流16という。
いま,LWSの特殊な場合として,次式で定められる汎関数Ēを最小化する問題を考える。
![]()
ここで,K¯は指定されたガウス曲率である。詳細は省略するが,曲面の法線方向の変分ψに対して,平均曲率の積分と体積の第一変分は,次式で表される。
![]()
したがって,Ēの第一変分は
![]()
となり,Euler-Lagrange の方程式は
![]()
のように導かれる。したがって,を単位法線ベクトルに乗じたベクトル(ガウス曲率流)にしたがって曲面を変形させることにより,曲面のいたるところでガウス曲率が指定K¯に一致するような曲面が得られる。

図1 離散曲面(多面体)の頂点での諸量の定義
ところで,ガウス曲率流を用いた数値解析によって曲面を生成するためには,曲面を三角形あるいは四辺形のメッシュに分割し,ガウス曲率や平均曲率を離散的に求める必要がある。例えば,曲面を三角形メッシュで離散化し,頂点iに接続する辺と面の諸量を図1のように定義すると,ガウス曲率Kiと平均曲率ベクトルHiは次のように定義できる。

ここで,
は頂点iの位置ベクトル,
は図1のオレンジ色の領域(ボロノイ領域)の面積,
は頂点i,j,kに接続する面,
Tiは頂点iに接続する面の集合,
Niは頂点iと辺で接続される頂点の集合である。
KiとHiの定義にはさまざまな表現があり,Gauss-Bonne の定理や Steiner の定理を満たすことが重要である7-17。 平均曲率の大きさはHiのノルムであり,その符号はHiの方向によって定まる。式 (6)においてで割らない場合は,ガウス曲率や平均曲率の積分の際にを乗じないで総和をとる。

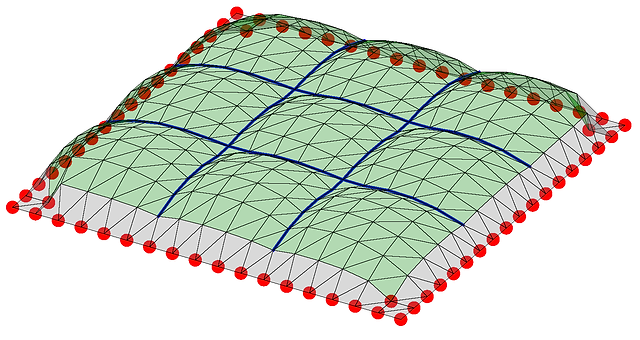
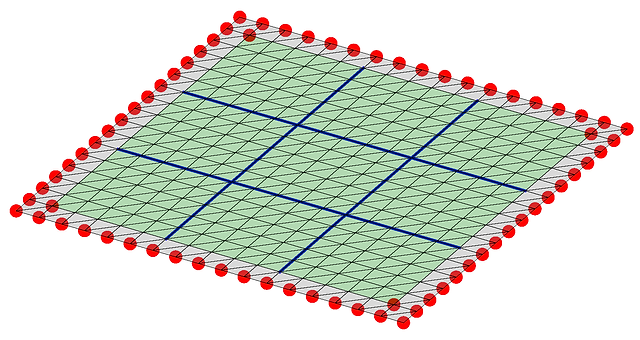
図2 正方形の境界を有する区分的ガウス曲率一定曲面の生成例¹¹
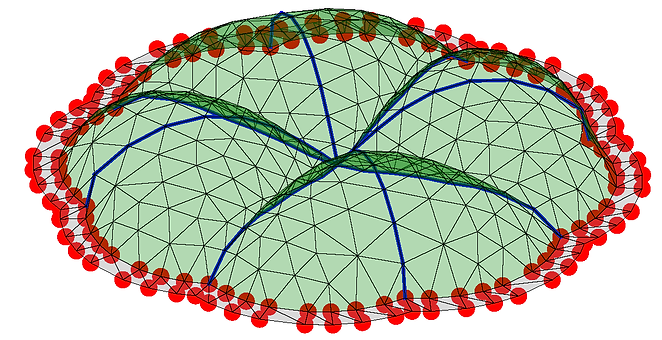
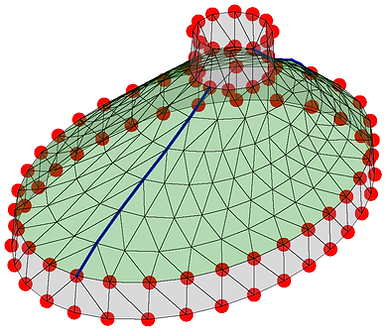
図3 曲線状の境界を有する区分的ガウス曲率一定曲面の生成例¹¹
3.ガウスマップを用いた離散曲面の形状設計
曲面のパラメータ定義に依存しない特性量を幾何学的不変量といい,勾配や単位法線ベクトルに加えて,主曲率で定義されるガウス曲率,平均曲率やそれらの関数が挙げられる。これらの不変量を用いて設計された曲面の代表例は,可展面と極小曲面である。1990年代初めに,さまざまな不変量を用いた曲面の設計法が提案され¹⁸,その応用についてtraverse4で紹介している19-20。ここでは,離散微分幾何学で定義される不変量とガウスマップを用いて,さまざまな曲面を生成する手法を紹介する12。
いま,設計しようとしている主曲面(primary surfaceあるいはdesign surface)の幾何学的不変量を用いて定義される曲面を随伴曲面(derived surface)といい,その代表例として,オフセット曲面やガウスマップが挙げられる。前者は図4(a)に示すように主曲面から等距離にある曲面であり,後者は図4(b)に示すように主曲面の単位法線ベクトルで構成される曲面である。
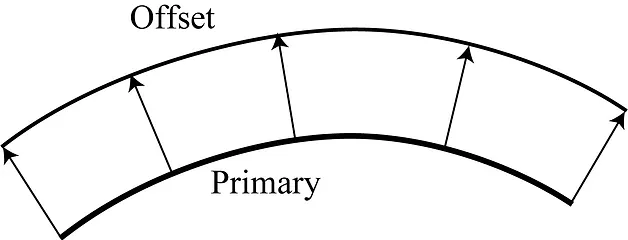
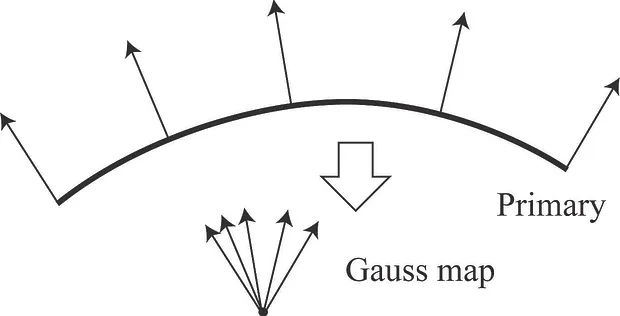
図4 筒状曲面の随伴曲面の例
図5の左図ような三角形メッシュの1つの面(グレーの領域)を考え,その3つの頂点での単位法線ベクトルの始点を同一の点に移動すると,右図のような三角形の面が構成される。すなわち,主曲面の単位法線ベクトルを頂点において式(7)で定義すると,ガウスマップは主曲面と同位相の三角形メッシュをもち,その面積を容易に計算できる。一方,法線ベクトルを辺や面で定義すると,ガウスマップを同位相の多面体で定義するのは困難であり,後述のようなガウス曲率や平均曲率を用いたガウスマップの拡張も難しい。

図5 三角形メッシュ多面体の1つの面のガウスマップ
ところで,特殊な形状の離散曲面(多面体)では,ガウスマップは三角形メッシュにはならない。例えば図6(a)のような筒状曲面や図6(b)のような区分的平面では,ガウスマップは図に示すように線分に退化し,その面積は0になる。したがって,ガウスマップの面積を最小化することによって,筒状の曲面あるいは区分的平面などの区分的可展面を生成することができる。


図6 筒状曲面と区分的平面のガウスマップ
四隅を固定した初期曲面をランダムに生成し,ガウスマップの面積を最小化して得られた曲面の例を図7(a)-(d)に示す。各図において左に曲面形状,右に勾配と逆向きのベクトルを示している。(d)は2枚の平面で構成される屋根であり,(a), (b), (c)はその四隅に勾配の大きい平面を付加した形式である。

次に,単純なガウスマップではなく,単位法線ベクトルn にとの関数を乗じた曲面の面積を最小化して得られた曲面を図8(a)に示す。曲面の面積は,文献18においてrolling metricとして定義され,それを最小化することによって筒型の曲面が得られる。図8(b)の立面図および図8(c)の勾配からわかるとおり,中央の筒型の曲面と両側の錐型の曲面で形成された区分的可展面が得られている。


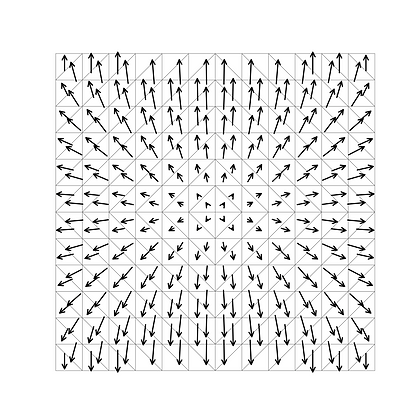
図8 曲面の面積最小化によって得られた曲面¹²
4.おわりに
本稿では,離散微分幾何学の手法を用いて曲面を生成する例を紹介した。コンピュータの能力の発展により,離散微分幾何学による手法はますます建築の形状設計において利用されるものと期待される。連続体シェル構造ではなくラチス屋根構造を設計・施工する際には,パネルの平面性が重要であり,PQメッシュ(planar quadrilateral mesh)21やcircle packingなどの手法に加えて,剛体折紙で開発されたさまざまな手法を利用することができる。また,ラチス部材の平面性も実現するため,edge offset曲面を利用することもできる22。さらに,シェルの形態や釣合い条件を定める複雑な微分方程式を差分法や最適化手法によって離散的に解くことも容易になってきている23。この分野の最先端の研究は,Advances in Architectural Geometry24などのシンポジウムで活発に発表されており,今後の離散的な手法の発展が期待される。
<参考文献>
1. G. R. Jensen, E. Musso and L. Nicolodi, Surfaces in Classical Geometries: A Treatment by Moving Frames, Springer, 2016.
2. L. Piegl and W. Tiller, The NURBS Book, Springer, 1995.
3. G. Farin, Curves and Surfaces for CAGD: A Practical Guide, Morgan Kaufmann, 5th ed., 2001.
4. 崔 京蘭, 大崎 純, 可展面を組合せた自由曲面の近似設計システムの開発, 日本建築学会技術報告集, Vol. 25(59), pp. 123–128, 2019.
5. S. Fujita and M. Ohsaki, Shape optimization of free-form shells using invariants of parametric surface, Int. J. Space Struct., Vol. 25, pp.143–157, 2010.
6. A. I. Bobenko, P. Schröer, J. M. Sullivan and G. M. Ziegler (Eds.), Discrete Differential Geometry, Birkhäuser, 2008.
7. A. I. Bobenko and Y. B. Suris, Discrete Differential Geometry: Integrable Structure, American Mathematical Society, 2008.
8. U. Pinkall and K. Polthier, Computing discrete minimal surfaces and their conjugates, Experimental Mathematics, Vol. 2, pp. 15–36, 1993.
9. E. Grinspun, Discrere Differential Geometry: An Applied Introduction, Course Notes, SIGGRAPH 2006, 2006.
10. 設計の新パラダイムを拓く新しい離散的な曲面の幾何学, http://ed3ge.imi.kyushu-u.ac.jp/
11. K. Hayashi, Y. Jikumaru, M. Ohsaki, T. Kagaya and Y. Yokosuka, Discrete Gaussian curvature flow for piecewise constant Gaussian curvature surface, Computer-Aided Design, Vol. 134, Paper No. 102992, 2021.
12. M. Ohsaki and K. Hayakawa, Non-parametric shape design of free-form shells using fairness measures and discrete differential geometry, J. Int. Assoc. Shell Spatial. Struct., Vol. 62(2), pp. 93–101, 2021.
13. J. A. Gálvez, A. Martínez and F. Milán, Linear Weingarten surfaces in R3, Monatshefte für Mathematik, Vol. 138, pp. 133–144, 2003.
14. X. Tellier, C. Douthe, L. Hauswirth and O. Baverel, Linear Weingarten surfaces for conceptual design of double-curvature envelopes, In: Proc. fib Conceptural Design Symposium 2019, Madrid, 2019.
15. M. Desbrun, M. Meyer, P. Schroder and A. H. Barr, Implicit fairing of irregular meshes using diffusion and curvature flow, ACM SIGGRAPH’99, pp. 317–324, 1999.
16. H. Zhaoa and G. Xub, Triangular surface mesh fairing via Gaussian curvature flow, J. Comp, Appl. Math., Vol. 195, pp. 300–311, 2006.
17. X. D. Gu and S.-T. Yau, Computational Conformal Geometry, International Press, 2008.
18. T. Rando and J. A. Roulier, Designing faired parametric surfaces, Comput-Aided Des., Vol. 23, pp. 492–497, 1991.
19. M. Ohsaki and M. Hayashi, Fairness metrics for shape optimization of ribbed shells, J. Int. Assoc. Shell and Spatial Struct., Vol. 41(1), pp. 31–39, 2000.
20. 大崎 純,曲線の滑らかさと力学,Traverse 4, 新建築学研究, Kyoto University Architectural Journal, pp. 47–54, 2003.
21. Y. Liu, H. Pottmann, J. Wallner, Y.-L. Yang and W. Wang, Geometric modeling with conical meshes and developable surfaces, ACM Trans. Graphics, Vol. 25(3), pp. 681–689, 2006.
22. H. Pottmann, P. Grohs and B. Blaschitz, Edge offset meshes in Laguerre geometry, Adv. Comput. Math., Vol. 33, pp. 45–73, 2010.
23. 堺 雄亮, 大崎 純, 膜応力の平面投影成分を用いた自由曲面シェルのノンパラメトリック形状設計法,日本建築学会技術報告集, Vol. 27, No.66, pp.1098–1103, 2021.
24. L. Hesselgren, A. Kilian, S. Malek, K.-G. Olsson, O. Sorkine-Hornung and C. Williams (Eds.), Advances in Architectural Geometry, Klein Publishing GmbH, 2018.