魅力的な曲面形状|大崎 純
Aesthetically attrractive surface shape | Makoto OHSAKI
建築構造力学の魅力
いうまでもなく,「惹かれるもの」は人によって異なる。筆者は,子供のころから機械のしくみに惹かれて,使えなくなった機械があれば必ず分解していたのを覚えている。高校生のときも純粋な理系だったので,建築のデザインに魅力を感じて建築学科に入学したわけではない。単に父親が建築関係の仕事をしていたので,工学部の中で身近な建築学科を受験したに過ぎない。したがって,入学時から構造系志望であった。いま受験するならば,たぶん機械工学か航空宇宙工学を志望したと思う。
建築を志す学生のほとんどは,意匠系や計画系に興味を持っていることは十分に理解しているが,建築の力学にも,意匠と同じような魅力を感じることもできる。筆者は,卒業研究でシェル構造の力学の研究をはじめて,修士論文からは構造最適化の研究を40年以上続けている。その間,骨組構造の解析や耐震設計の研究も行ってきたが,やはりシェル構造や空間骨組構造の力学的に最適化された形態の魅力が,筆者の研究を支えてきたといっても過言ではない。例えば,F1のレーシングカーや航空機は一般には美しさを感じる対象ではないが,筆者にとっては究極的に美しく魅力的なものであり,例えばアメリカのオーバルコースを延々と走り続ける自動車レースを2時間見続けて楽しむこともできる。
一方で,建築の曲面構造は最先端の力学で最適化されたものではない。しかし,優れた建築家と構造家によって設計されたシェル構造からは,微妙な力のバランスや流れを五感で感じることもできるかもしれない。もちろん膜構造やケーブル補強骨組などの張力構造での力のバランスは非常に魅力的である。しかし,一般には建築の曲面構造から力学的魅力を感じる人は少ないので,やはり形状の意匠的魅力,すなわち美しさが重要である。
惹かれる曲面形状
曲面の美しさあるいは魅力は極めて主観的であり,客観的に魅力的な曲面は存在しない。しかし,機械設計や工業デザインの分野で,魅力的な曲面や曲線に関する研究は古くから存在する。曲線に関しては,曲率対数分布図(グラフ)といわれる曲率半径の変化に関するグラフの滑らかさが,曲線の美しさの1つの指標であり,それが線形であるような曲線を,対数型美的曲線(log-aesthetic curve)という。対数型美的曲線では曲率半径のべき乗が弧長の線形関数であり,その例を図1に示す。特殊な場合として,図2のような対数螺旋があり,巻貝の形状として知られている。Haradaら[1]は,自動車のボンネットの曲線が対数型美的曲線で近似できることを示した。三浦ら[2]は,それを発展させて数学的な意味づけを行った。最近になって,梶原らの研究グループ[3]によって,対数型美的曲線の自己相似性や曲面への展開のための研究が進められている。

惹かれる形は,形状の滑らかさと関係が深い。計算機を用いた形状設計(Computer-Aided Geometric Design, CAGD)の分野でも,1990年代から滑らかさの計量に関する研究が行われている。Roulier and Rando [4]は,丸さ(roundness),回転性(rolling),平面性(planeness)などさまざまな滑らかさの計量を提案した。Ohsaki and Hayashi [5]は,滑らかさの計量を用いた建築のシェル構造の設計法を提案した。滑らかさの計量は,一般に,曲面の幾何学的不変量あるいは代数不変量(ガウス曲率,平均曲率,主曲率など)によって定式化される。Fujita and Ohsaki [6]は,代数不変量を用いた形状設計法を提案した。
建築のいわゆる自由曲面シェルはベジエ曲面やNURBSなどのパラメトリック曲面でモデル化されるが,構造解析や施工の段階では離散的なメッシュやパネルが用いられる。したがって,最初から離散化された曲面(多面体)を対象とするのが望ましく、離散曲面の滑らかさの計量を用いた設計法が,Ohsaki and Hayakawa [7]によって提案されている。Rollingとroundnessの計量を最小化する形状を図3, 4に示す。一方で,1つの方向に直線の母線を持つ曲面も,魅力的かつ施工性に優れた曲面であり,線織面や可展面を用いた設計法[8, 9]が提案されている。それらの例を図5, 6に示す。
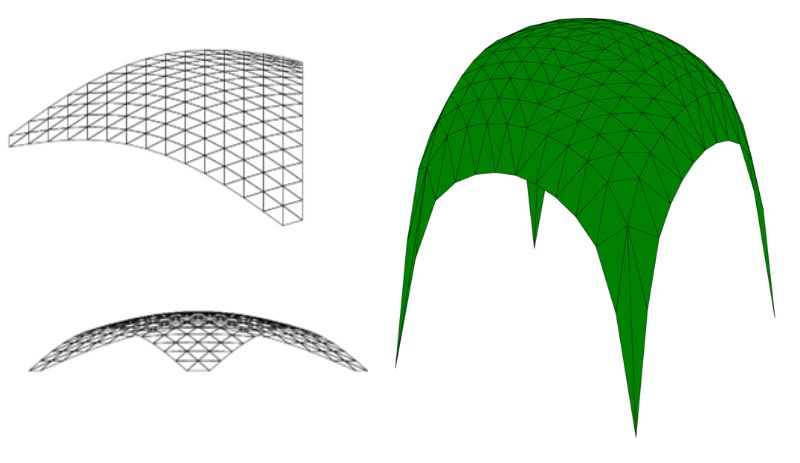
図3 剛性と丸さのトレードオフを考慮した形状(立面図)(左下)
図4 Roundnessの計量を最小化する曲面(右)

図6 可展面を接続したシェル(右)
工学の分野での美しさの定量化や客観的評価は,感性工学の分野で研究されている。「感性」はsensibilityに対応する学術用語として明治時代から使用されていたが,「感性工学」は,1980年代に日本の自動車会社によって心理評価と統計を組み合わせた手法として開発され、長町三生によって創始されたといわれている[10]。その後,工学全般のデザインに関わるKansei Engineeringとして,世界に広まった。1990年代になって日本学術会議でも議論され,1998年に「日本感性工学会」が設立された。
日本建築学会では,情報システム技術委員会の下に感性工学システム研究小委員会が2005年に設立され,2008年に,「都市・建築の感性デザイン工学」[11]を出版している。建築は,視覚のみならず,音,熱,光,振動,嗅覚などのあらゆる面で,感性と関係している。力学的感性についても,構造委員会・応用力学小委員会の下の力学的感性小委員会で検討され,「建築形態と力学感性」が出版された[12]。力学的には,形態のみならず,安定性,剛性,地震や風に対する応答,軽量性なども感性に関係する。しかし,感性は極めて主観的なものであるため,科学的な方法論の確立は難しく,SD法や主成分分析などの古典的な方法が多く用いられている。最近ではさまざまな機械学習の方法が利用され,今後の発展も期待できる。
建築構造の美しさについては,坪井善勝の「構造の美しさは合理の近傍にある」という言葉が有名であるが,何らかの著作で解説されているわけではないので,いろいろな表現で伝えられている。また,その解釈にも揺らぎがあるが,「美しさは合理のみからは生まれない。構造的合理性から少し外れても構造的処置は可能である」[13]という解釈が概ね正しそうである。建築形態が構造的合理性だけで決まらないのは当然であるが,究極的に構造合理性を達成した形態を美しいと思う人もいるかもしれない。
参考文献
[1] T. Harada, F. Yoshimoto and M. Moriyama, An aesthetic curve in the field of industrial design, Proc. 1999 IEEE Symposium on Visual Languages, pp. 38-47, 1999.
[2] 三浦憲二郎, 吉田典正, 美しい曲線・曲面の定式化へ向けて, 精密工学会誌, Vol. 73(12), pp. 1295-1299, 2007.
[3] 科学技術振興財団(JST), CREST, 設計の新パラダイムを拓く新しい離散的な曲面の幾何学, 代表: 梶原健司, 2019~2025. https://ed3ge.imi.kyushu-u.ac.jp/
[4] J. A. Roulier and T. Rando, Measures of fairness for curves and surfaces, in: Designing Fair Curves and Surfaces: Shape Quality in Geometric Modeling and Computer-Aided Design, N. S. Sapidis Ed., Philadelphia: SIAM, pp. 75-122, 1994.
[5] M. Ohsaki and M. Hayashi, Fairness metrics for shape optimization of ribbed shells, J. Int. assoc. Shells and Spatial Struct., Vol. 41(1), pp. 31-39, 2000.
[6] S, Fujita, M. Ohsaki and K. Seki, Shape optimization of latticed shells consisting of ruled surface, Proc. IASS Symposium 2016, Tokyo, Int. Assoc. Shell and Spatial Struct., Paper No. CS6M-1251, 2016.
[7] M. Ohsaki and K. Hayakawa, Non-parametric shape design of free-form shells using fairness measures and discrete differential geometry, J. Int. Assoc. Shell Spatial. Struct., Vol. 62, No. 2, 93-101, 2021.
[8] K. Seki, M. Ohsaki and S. Fujita, Shape optimization of ruled surface considering static stiffness, Proc. 11th Asian Pacific Conf. on Shell and Spatial Struct (APCS 2015), pp. 269-274, 2015.
[9] 崔 京蘭,大崎 純, 中村奎吾,可展面を接続した自由曲面シェル構造の形状最適化, 日本建築学会構造系論文集, Vol. 82, No. 737, pp. 1137-1143, 2017.
[10] 日本デザイン学会 編, デザイン科学事典, 感性工学, pp. 74-79, 丸善, 2019.
[11] 日本建築学会 編, 都市・建築の感性デザイン工学, 朝倉書店, 2008.
[12] 日本建築学会 編, 建築形態と力学的感性, 丸善, 2014.
[13] 坪井義昭,川口 衞,佐々木睦朗,大崎 純, 植木隆司,竹内 徹,川端昌也,川口健一,金箱温春,力学・素材・構造デザイン,建築技術, 2012.
大崎 純(おおさき・まこと)
京都大学大学院工学研究科教授。国際シェル空間構造学会理事。研究分野は,構造最適化,シェル・空間構造・張力構造の解析と設計,構造物の非線形解析・安定解析など。構造物の最適なかたちに興味を持ち,最近は,離散微分幾何学を用いた形状設計,構造設計と最適化への機械学習の利用などの研究を行っている。