【大崎・張研究室】traverse24 Project

折紙工学と建築への応用

特定助教　早川 健太郎　

はじめに

折紙は日本や中国の伝統的な手習いや芸術として国際的に広く認知されている。一方、折紙の「折る」という操作や折りにより得られる形状の数学的、工学的な研究も盛んに実施されている。数学のなかでも計算幾何学とよばれる分野では「計算折紙（computational origami）」と称して、どのような折線パターンならば折ることができるのか、与えられた形状を実現するには折線パターンをどのようにデザインするのか、などの多くの問題が提示され、折紙の数理的な扱いが研究されている[1,2]。計算折紙では、紙のような２次元の物体の折りだけでなく、１次元（リンケージ）や３次元（多面体）の物体の折りも研究対象となっている。

工学分野では、折紙の数理的な取り扱い方法が整備されるにともない、１枚以上の平坦な紙を折ることで２次元や３次元の様々な形状を作り出す操作や、折りによって得られる形状の物理的性質を工学的に生かす「折紙工学（engineering origami,structural origami）」が近年盛んに研究されている[3,4,5]。航空宇宙、自動車、ロボット、医療、建築、服飾、プロダクトデザインなど様々な場面、スケールで折紙の応用例がある。次節では、建築に限らない幅広い分野での折紙の応用例を紹介する。次節で紹介する折紙の応用例は大きく以下の３つに分類される。

１. 折り動作を応用した繰り返し変形可能な構造物

２. 折り動作を用いた新たな製造・施工法

３. 折りにより得られる形状がもつ特殊な機械的性質の利用

さらに、本稿では以下に示す、著者らの研究グループによる折 紙に関連した研究成果などの一部を紹介する。

• 剛体折紙の数理モデルの開発

• 剛体折紙を用いた曲面近似

• 剛体折紙の形状生成法を用いた建築設計（丸山悠斗：2021 年度卒業設計）

折紙の工学的応用例

折紙の工学的応用例の１つ目として、小さく折りたたんで運搬し、目的地で所定の形状に展開できる構造物が挙げられる。人工衛星に搭載されるソーラーパネル[6]や、人体の血管内に留置されるステントグラフト[7]、パビリオンや緊急時のシェルター[8,9]などへの応用が提案されている。こうした例では、繰り返し折り畳み・展開可能であることや硬い素材で面を構成することを求められる場合が多く、「剛体折紙」が多くの場合で用いられる。剛体折紙は折り過程で面が変形せず、折線の回転のみを許容するモデルで、このような厳しい条件下でも折ることのできるものを「剛体折り可能」であるという[10]。この条件下での剛体折紙は外力に抵抗せず、ひずみエネルギーがゼロのまま大きく変形可能な不安定構造である。このような不安定構造は「メカニズム」とよばれ、剛体折紙のように剛な面（パネル）を折線（ヒンジ）で接続したものだけでなく、剛な梁部材をヒンジやピンで接続したリンケージなどがある。剛体折り可能な折線パターンの例としては、図１(a)のミウラ折り、図１(b)のヨシムラパターン、図１(c)のwaterbomb tessellation、図１(d)のReschのパターンなどが挙げられる。剛体折紙の変形機構は、パネルの物理的な干渉を無視すればその薄さや柔らかさに依存しない。したがって、上記の例のように医療器具から建築物まで幅広いスケールの変形機構に応用でき、パネルに金属や木材など様々な素材を利用できるなど、産業応用の可能性が高い。一方、ある状態から別の状態へ連続的に剛体折り可能な折線パターンを得ることは容易ではない。剛体折紙の工学的応用においては、１)与えられた折り線パターンの剛体折り可能性の判定、２)剛体折りによる変形プロセスのシミュレーションや、３)剛体折り可能性を保証しつつ折紙の３次元形状を設計するための手法の開発が重要な課題であり、著者らの研究グループでは主にこれら３つの課題に取り組んでいる。

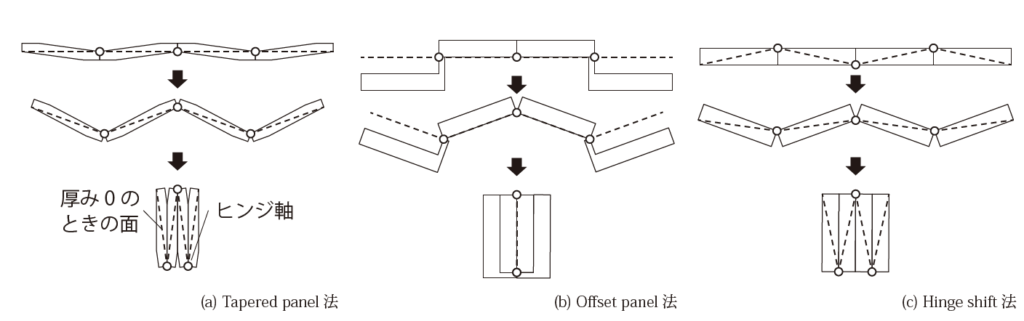
加えて、剛体折紙を実構造物へ応用するためには素材の厚みの処理も重要な課題である。パネルの厚み処理には図２に示すようなTapered panel法[11]、Offset panel法[12]、Hinge shift法[13]などが提案されている。図中の点線は厚みが０であると仮定した場合のパネルの位置を表しており、完全に展開した状態（上段図）でTapered panel法とOffset panel法ではヒンジの回転軸が同一平面にあるのに対して、Hinge shift法ではヒンジが同一平面上にない。したがって、平面上でデザインした剛体折紙の折り線パターンに前者２つではそのままパネル厚を与えればよいのに対し、後者では変形メカニズムを得るために特殊な処理が必要である。また、図２下段のように、Tapered panel法とHinge shift法では点線で表される厚み０の面がパネルの干渉により完全には折りたたまれないのに対し、Offset panel法では完全に折りたたむことができる。厚み処理に関するさらなる情報はサーベイ論文[14]を参照するとよい。

応用例の２つ目は、シート状の平坦な素材から折り動作により効率的に所定の立体形状をもつ製品、構造物を製造、施工する手法であり、「折紙ハニカム」とよばれる高剛性なサンドイッチパネルのコア材の製造法[15]に代表される。折紙の技術を応用することで既存の折り曲げ加工技術を応用しつつ、切削などのコストが高い加工なしにさまざまな形状のコア材を製造できる。また、加工機無しで立体形状に折り上げる「自己折り」も盛んに研究されている。自己折りはシート状の素材に適切な加工を施し、加熱するなどの外的刺激を与えて折線部分を駆動することで立体形状に折り上げる手法である。複雑な折り操作を必要としないため、技術がない者でも容易に複雑な立体形状を製作可能なこと、人間の手や加工機が入らないような場所でも折り動作を用いた立体形状を実現可能なことなどの利点がある。形状記憶合金などの金属材料を用いた手法[16]のほか、熱収縮ポリマーのシートに折線パターンを印刷して自己折りを実現する手法[17]などが提案されている。

応用例の３つ目は、薄い素材に折り目をつけることで様々な機械的性質をもつ構造物を実現する試みである。身近な例では、トタン屋根などにみられる波板、一部の缶に採用されているダイヤモンド状のデザインなどが挙げられる。これらの例では折り目を導入することで、同じ厚さの折り目の無い板に対して面外の剛性を高めている。さらに、折紙を用いた衝撃吸収機構[18,19]や折紙メタマテリアル[20,21]が提案されている。前者では、折り目を入れた筒状の構造物が軸方向に潰れることで自動車等の衝突時の衝撃を吸収する。折り目によって変形が誘導されることで構造物全体が効率的に潰れ、折り目が無い場合と比較してエネルギー吸収量の増大が期待される。後者の例では、折線パターンをデザインすることで構造物全体の剛性分布やポアソン比などを操作し、通常の均一な物質では実現しえないような機械的特性をもつ構造物を実現する。

図版作成：早川 健太郎

参考文献

[1] E. D. Demaine and J. O’Rourke, Geometric folding algorithms: linkages, origami, polyhedra, Cambridge University Press, 2007

[2] R. Uehara, Introduction to Computational Origami, Springer, 2020

[3] 田中浩也，舘知宏，コンピュテーショナル・ファブリケーション　「折る」「詰む」のデザインとサイエンス，彰国社，2020

[4] M. Meloni, J. Cai, Q. Zhang, D.S. Lee, M. Li, R. Ma, T.E. Parashkevov, and J. Feng. Engineering origami: A comprehensive review of recent applications, design methods, and tools, Adv. Sci., Vol. 8, paper no. 2000636, 2021.7

[5] 野島武敏，折紙工学入門，化学同人，2023

[6] S.A. Zirbel, R.J. Lang, M.W. Thomson, D.A. Sigel, P.E. Walkemeyer, and B.P. Trease, S.P. Magleby, and L.L. Howell, Accommodating thickness in origami-based deployable arrays, J. Mech. Des., Vol. 135, No. 11, paper no. 111005, 2013.10

[7] K. Kuribayashi, K. Tsuchiya, Z. You, D. Tomus, M. Umemoto, T. Ito, and M. Sasaki, Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil, Mater. Sci. Eng. A, Vol. 419, No. 1, pp. 131–137, 2006.3

[8] N. De Temmerman, M. Mollaert, T. Van Mele, and L. De Laet, Design and analysis of a foldable mobile shelter system, Int. J. Space Struct., Vol. 22, No. 3, pp. 161–168, 2007.9

[9] K. Ando, B. Izumi, M. Shigematsu, H. Tamai, J.

Matsuo, Y. Mizuta, T. Miyata, J. Sadanobu, K. Suto and T. Tachi,

Lightweight rigidly foldable canopy using composite materials,

SN Appl. Sci., Vol.2, article no. 1994, 2020.11

[10] 舘知宏，剛体折紙メカニズム，日本ロボット学会誌，

Vol. 34, No. 3, pp. 184–191, 2016.4

[11] T. Tachi, Rigid-Foldable thick origami, in Origami5,

CRC Press, pp.253–264, 2011

[12] B.J. Edmondson, R.J. Lang, S.P. Magleby, and L.L.

Howell, An offset panel technique for thick rigidly foldable

origami, in Proc. ASME 2016 International Design Engineering

Technical Conferences and Computers and Information in

Engineering Conference, paper no. DETC2014-35606, 2016.8

[13] M. Trautz, and A. Künstler, Deployable folded plate structures-Folding patterns based on 4-fold-mechanism using stiff plates, in Proc. IASS Symposium 2009, pp. 2306–2317, 2009.9

[14] R.J. Lang, K.A. Tolman, E.B. Crampton, S.P. Magleby, and L.L. Howell, A review of thickness accommodation techniques in origami-inspired engineering, Appl. Mech. Rev., Vol. 70, pp. 010805-1–010805-20, 2018.1

[15] T. Nojima and K. Saito, Development of newly designed ultra-light core Structures, JSME International Journal Series A Solid Mechanics and Material Engineering, Vol. 49, No. 1, pp. 38–42, 2006.7

[16] N. Lazarus, G.L. Smith and M.D. Dickey, Self-folding metal origami, Advanced Intelligent Systems, Vol. 1, No. 7, paper no. 1900059, 2019.8

[17] K. Narumi, K. Koyama, K. Suto, Y. Noma, H. Sato, T. Tachi, M. Sugimoto, T. Igarashi, and Y. Kawahara, Inkjet 4D Print: Self-Folding Tessellated Origami Objects by Inkjet UV Printing, ACM Trans. Graph., Vol. 42, No. 4, article no. 117, 2023.8

[18] J. Ma and Z. You, Energy absorption of thin-walled square tubes with a prefolded origami pattern-part I: Geometry and numerical simulation, J. Appl. Mech., Vol. 81, No. 1, article no. 011003, 2013.8

[19] C. Zhou, Y. Zhou, and B. Wang, Crashworthiness design for trapezoid origami crash boxes, Thin-Walled Struct., Vol. 117, pp. 257–267, 2017.8

[20] J.L. Silverberg, A.A. Evans, L. McLeod, R.C. Hayward, T. Hull, C.D. Santangelo, and I. Cohen, Applied origami: Using origami design principles to fold reprogrammable mechanical metamaterials, Science, Vol. 345, No. 6197, pp. 647–650, 2014.8

[21] P.P. Pratapa, K. Liu, and G.H. Paulino, Geometric mechanics of origami patterns exhibiting Poisson’s ratio switch by breaking mountain and valley assignment. Phys. Rev. Lett., Vol. 122, article no. 155501, 2019.4