【大崎・張研究室】traverse24 Project

剛体折紙を用いた曲面近似

特定助教　早川 健太郎

はじめに

ここでは著者らによる剛体折紙の形状生成法[30,31]の概要を紹介する。文献[30,31]では、剛体折紙の変形機構を応用し、平面から剛体折りにより施工可能な屋根構造等を実現することを目的として、与えられた曲面（以下、目標曲面）を剛体折紙で近似する手法を提案している。目標曲面を近似することは、意匠性や建築物の内部構成、周辺環境をもとにした設計者の要求を満たすために重要である。既往研究ではミウラ折りに代表される四辺形メッシュ[37,38]やwaterbomb tessellation[39]、Reschのパターン[40]などの折線の接続関係が周期的かつ固定された折線パターンを用いる例が多い。一方、著者らの提案手法[30,31]では折線パターンを特定のものに限定せず剛体折紙の形状を生成できる。本手法では、与えられた目標曲面と剛体折紙曲面の間の非負の近似誤差関数を最小化することで折紙曲面の形状を得る。その際、折紙曲面が面を変形させずに接続状態を変えることなく平面へ展開可能であるための条件（以下、展開可能条件）を課す。近似誤差関数は目標曲面と折紙曲面の間の距離、面積の誤差、および法線ベクトルの誤差を考慮して定義する。なお、本稿では剛体折紙を構成する多面体を「折紙曲面」とよぶ。図６に示すように折紙曲面上には辺に沿った切り目を適宜配置することで、切り目がない場合よりも近似精度を高める。切り目は図７に示すように立体形状では閉じており、展開図上でひらくまたは局所的な面の重なりを生じる。形状生成の過程で折線を順に削除しながら繰り返し近似誤差最小化を行うことで、変形自由度が小さく、折り変形の制御が容易な解形状を生成し、建築構造への応用に適した剛体折紙の形状と折線パターンを獲得する。削除する折線はフレームモデルの微小変形メカニズムにもとづき決定する。

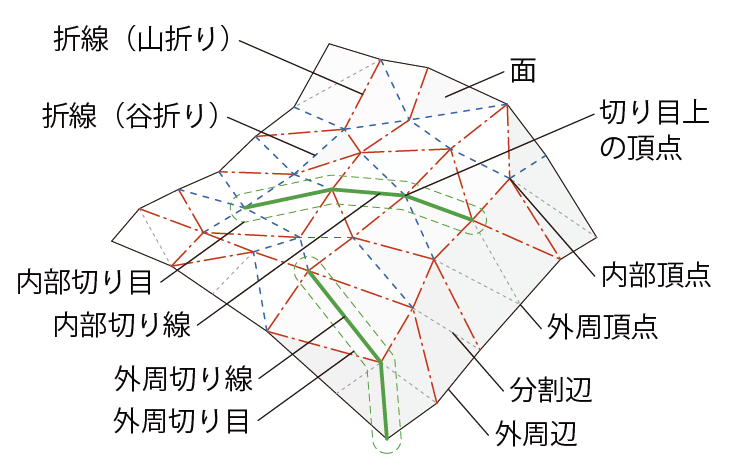
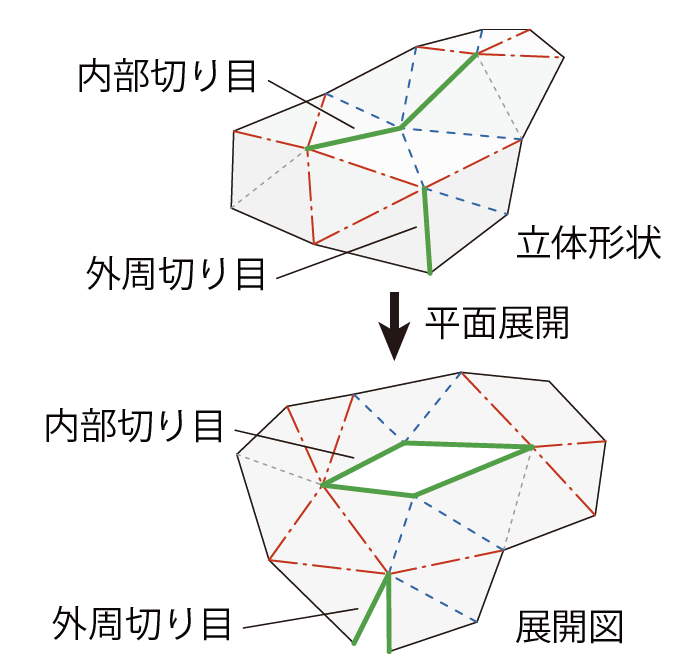
展開可能条件

折紙曲面は三角形メッシュで表現される。図６に示すように三角形メッシュの辺を、接続する２面の相対的な回転を許容する「折線」、接続する２面が常に同一平面上にあり剛体折紙の多角形面を三角形分割している「分割線」、切り目を構成する「切り線」、折紙曲面の外周境界上の「外周辺」に分類する。「切り目」は複数の連続した切り線の集合であり、切り目を構成する切り線の端部が外周に達しているものを「外周切り目」、それ以外を「内部切り目」とよぶ。切り線は、切り目のグラフ構造に着目した際に閉経路を持たず、平面展開時に折紙曲面が複数に分割されないように配置する。

本節では、折紙曲面の展開可能条件の定式化を結果のみ示す。それぞれの条件式の導出過程は文献[31]を参照すること。まず、切り線および外周辺の端点ではない内部頂点周りでの展開可能条件を示す。頂点jの周りの三角形面の集合をτj、面i∈τjの頂点jにおける内角をαi,jとするとき、内部頂点での展開可能条件は次式に示す頂点での離散ガウス曲率[41]が０であることである。

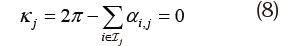
分割辺に接続する隣り合う２つの三角形面は平行である必要がある。したがって、ある分割辺を共有する三角形面i₁ i₂ の単位法線ベクトルをそれぞれn_i1,n_i2∈R³とおくと、分割辺での展開可能条件は以下のように書ける。

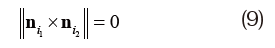
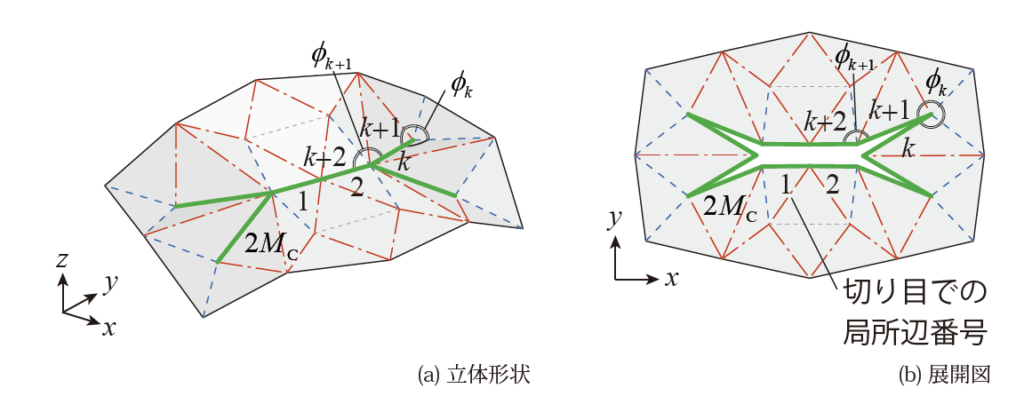
内部切り目では展開図上で切り線が１周回って閉じる必要がある。切り目での展開可能条件を定式化するため、図８(b)に示すように展開図において切り線に局所辺番号1,2,..,MCを反時計回りに与える。ただし、MCは立体形状での切り線の数である。このとき，図８(a)の辺kとk+1のように立体形状では同一の辺に２つの局所辺番号が与えられている。辺kとk+1の間の面の頂点周りの面の内角の和をφk、辺kの長さをlk、切り線τcの端点である頂点の集合をJcとおくと、内部切り目での展開可能条件は以下のようになる。

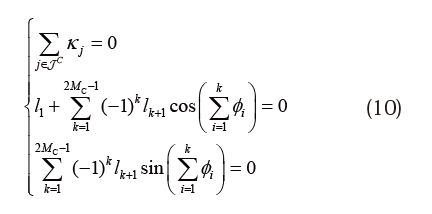
近似誤差関数

折紙曲面が目標曲面の「見た目」を近似するように近似誤差関数を定義する。図９に示すように、折紙曲面の頂点と目標曲面の間の距離が同じでも折紙曲面の見た目が大きく異なる場合があることから、目標曲面と折紙曲面の間の距離に加え、面積の誤差、および法線ベクトルの誤差に関する近似誤差関数を定義する。折紙曲面の頂点数をNV、頂点j(=1,…,NV )と目標曲面との距離をζj∈Rとするとき、折紙曲面の頂点と目標曲面の距離に関する近似誤差Fpを以下のように定義する。

また、折紙曲面の表面積を A∈R 、 目標曲面の表面積を A∈R として、表面積に関する近似誤差F_Aを以下のように定義する。

さらに、折紙曲面の三角形面の数をN_F、 三角形面i(=1,…,N_F)の単位法線ベクトルをn_i∈R³ 、 面iの３頂点を目標曲面に投影した点での目標曲面の単位法線ベクトルの平均をとった単位ベクトルをn_i∈R³として、法線ベクトルに関する近似誤差F_Nを以下のように定義する。

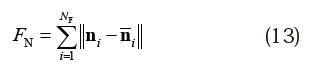
折紙曲面の形状はF_P、F_A、F_Nの重み付け和を展開可能条件の下で最小化する以下の最適化問題を解くことで得られる。

ここで、w_A,w_N∈Rは非負の重み係数である。また、最適化問題(14) の２つ目の制約条件は折紙曲面の面が点や線につぶれないために面の内角と辺長に課す上下限制約等である。形状生成の変数は、文献[30] ではフレームモデルの節点座標、文献[31] では目標曲面上に張られた２次元座標の値と目標曲面からのオフセット量である。

形状生成プロセス

形状生成プロセスは以下の通りであり、折線を削除しながら最適化問題(14) を繰り返し解くことで変形自由度の小さい折紙曲面を生成する。

１. 目標曲面を三角形分割し、切り線とする辺を選択する。

２. 最適化問題(14) を解く。

３. ２で展開可能条件を精度よく満たす解が得られた場合は4に、その他の場合は６に進む。

４. フレームモデルを用いて解の微小変形メカニズム解析を行い、回転できない折線（ロックした折線）が存在しない場合は５に、存在する場合は６に進む。

５. 削除可能な折線が存在する場合は削除する折線を１本または複数本選択し、選択された折線を分割辺に変更して２に戻る。その他の場合は７に進む。

６. 最後に分割辺に変更した辺を折線に戻し、戻した折線の他に削除可能な折線が存在する場合は新たに選択した折線を分割辺に変更して２に戻る。その他の場合は７に進む。

７. 得られた解形状の展開図を作成して、誤差無く平面展開可能であることを確認する。

８. 得られた解形状に対し、大変形解析による剛体折り過程のシミュレーションを実施して、剛体折りが可能であることを確認する。

上記の７、８は最適化問題(14)を解いて得られる形状が平面展開可能であるための必要条件のみを満たしており、実際に剛体折りによって平面へ誤差無く展開可能であるかが保証されないことから必要な過程である。また、４におけるロックした折線とは、式(7)による１次の微小変形メカニズムにおいて回転角変化量が０である折線（ヒンジ）である。ロックした折線が０でない折り角をもち、接続する２面が同一平面上にない場合、剛体折りによって解形状を平面に展開することができないため、削除する折線を変更する。したがって、最適化問題(14)を解く回数を減らし、効率よく剛体折紙の形状を生成するために、最適化問題(14)の解が得やすく、かつロックした折線が生じにくいような折線を５および６で選択して分割線に変更する必要がある。著者らはそのような折線の選択基準として、折線の折り角とフレームモデルの１次の微小変形メカニズムにおける折線に対応したヒンジの回転角変化量を用いた折線のスコアを提案している[30]。スコアの定式化は煩雑であり、ここには示さないが、スコアが小さい折線から順に削除することで、折り角のみを基準とした場合や微小変形メカニズムのみを基準とした場合、ランダムに折線を選択した場合と比較して、同じ数の折線を削除するために最適化問題(14)を解く回数を減らすことができている。

形状生成例

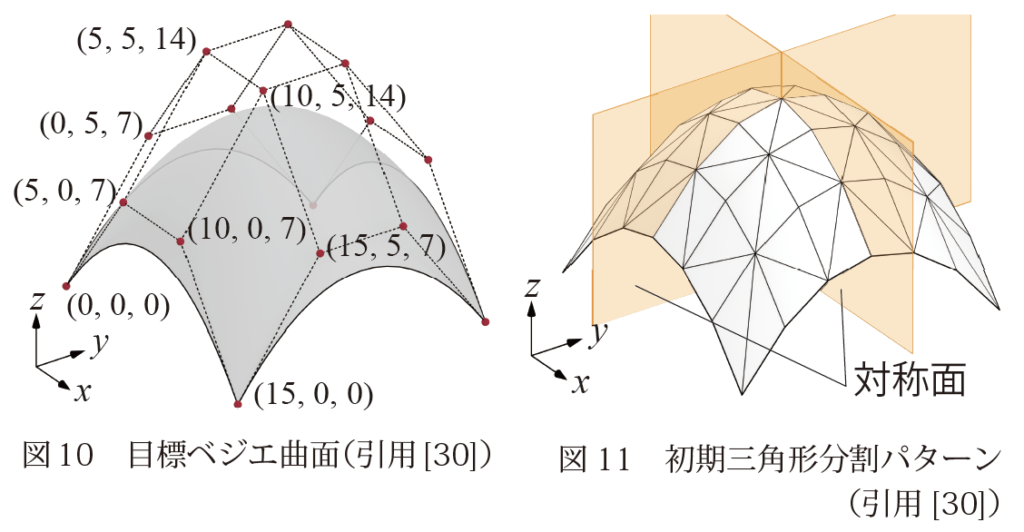
図10に示す制御点配置のベジエ曲面を目標曲面として形状生成を行う。初期三角形分割パターンは図11に示すとおりとし、xy平面とyz平面に平行な面に関する対称性を保つように解形状を求める。折線を削除する際には対称な位置に存在する２または４の折線を同時に削除する。近似誤差関数の重み係数はwA=0.2、wN=1.0とする。

図12に折線を20本削除した解形状を示す。図12(a)、(b)に示す解形状は共に十分な精度で平面展開可能かつ剛体折り可能である。切り目を導入しない図12(a)の解形状では、変形自由度は１であるが、外周付近で大きく折れ曲がっている。一方、外周部に切り目を導入した図12(b)の解形状では、変形自由度は９で切り目のない場合より大きくなっているが、近似誤差関数の値はおおよそ３分の１になっており、全体に凸な目標曲面に近い見た目の形状が得られている。このように、切れ目を導入することで変形自由度が大きくなる代わりに近似精度が高い折紙曲面が得られる。

参考文献

[37] L. Dudte, E. Vouga, T. Tachi, and L. Mahadevan, Programming curvature using origami tessellations, Nat. Mater., Vol. 15, pp. 583–588. 2016.1

[38] X. Dang, F. Feng, P. Plucinsky, R.D. James, H. Duan, and J. Wang, Inverse design of deployable origami structures that approximate a general surface, Int. J. Solids Struct., Vol. 234–235, article no. 111224, pp. 182–199, 2022.1

[39] Y. Zhao, Y. Endo, Y. Kanamori, and J. Mitani, Approximating 3D surfaces using generalized waterbomb tessellations, J. Comput. Des. Eng., Vol. 5, No. 4, pp. 442–448, 2018.10

[40] T. Tachi, Designing freeform origami tessellations by generalizing Resch’s patterns. J. Mech. Des., Vol. 135 No. 11, pp. 111066-1–111006-10, 2013.8

[41] J. M. Sullivan: Curvatures of Smooth and Discrete Surfaces, Discrete Differential Geometry, Oberwolfach Seminars, Vol. 38, pp. 175–188, 2008