【大崎・張研究室】traverse24 Project
剛体折紙の数理モデルの開発
特定助教 早川 健太郎
はじめに
剛体折紙の形状生成、構造解析をコンピュータ上で行ううえで適切な数理モデルを選択することは、剛体折り可能であるための条件や考慮する境界条件を正しく反映し、効率よく数値解析を実行するために非常に重要である。形状生成では、面の内角や隣り合う面の間の角度などの折紙の形状に関する幾何学的条件を必要十分に表現できることが求められる。また、構造解析では、剛体折紙の変形を表現する変数の選択、変数の適合条件(拘束条件)の定式化が計算効率や考慮可能な荷重条件、支持条件を大きく左右する。変数には剛体折紙の頂点座標や変位、折り角(折線に接続する2つの面の法線ベクトルのなす角)が用いられる場合が多く、これらの変数には、折り変形時に考慮される幾何学的・力学的な条件が満たされるよう適合条件が課される。
剛体折紙の解析の分類と用いられる数理モデル
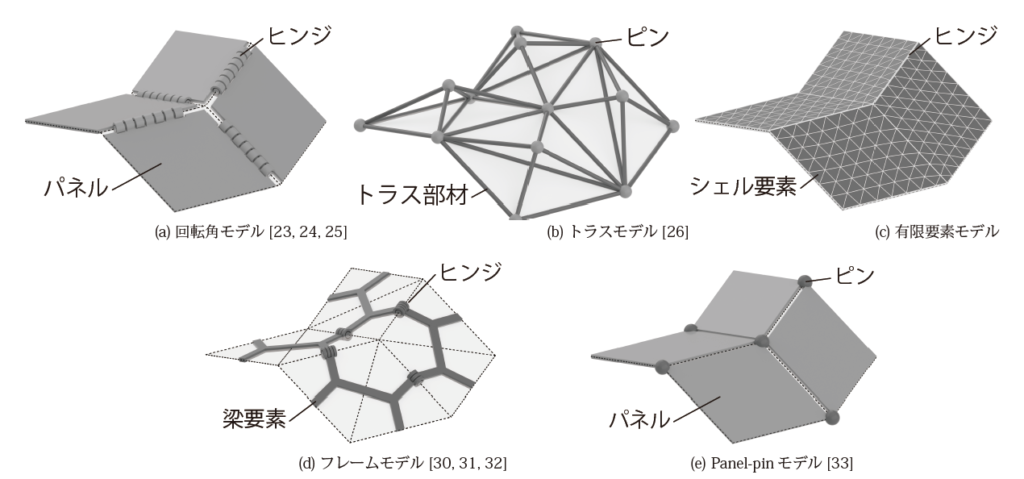
剛体折紙の構造解析は変位に課す適合条件の厳しさに応じて表1のように大きく3段階に分類できる[22]。最も剛体折紙の変形を理想化した解析は、剛体折紙本来の回転剛性を持たない折線部分の折り変形のみを許容する運動学、機構学的解析(表1の1行目)である。この解析では、剛体折紙の変形は折線の幾何学的な配置のみで決定され、外力などの力学的条件は考慮しない。このような条件では回転角モデル[23,24,25]が広く用いられている。回転角モデルは図3(a)に示すように物理的には剛なパネルを折線部分でヒンジ接合した数理モデルとして理解できる。変数は折り角であり、折り角は剛体折紙の頂点および穴の周囲で面が一周矛盾することなく接続するための適合条件式を満たす必要がある。このモデルを用いて剛体折紙の折り変形をシミュレートするソフトウェアとして、Rigid Origami Simulator[25]が公開されている。回転角モデルを用いると剛体折紙の変形状態を少ない変数で表現できる。一方、頂点座標が陽に与えられないため、形状を変数から直感的に把握することは困難であり、頂点位置を拘束したような解析は容易ではない。
現実の構造物へ剛体折紙を応用する場合には、折り変形を拘束するために頂点の変位拘束が与えられることが多い。したがって、頂点座標や頂点変位を変数とした図3(b)に示すトラスモデル[26]などが用いられる。トラスモデルでは、折り変形の過程で部材長が不変という幾何学的な適合条件が課される。頂点の位置が陽に表現されるため支持条件の導入が容易であるが,部材の不伸長条件で4以上の辺をもつ多角形面の変形を拘束するためには、図3(b)に示すように面外にも節点を配置して立体的に複雑に部材を組む必要がある。
剛体折紙は1つのパラメータで全体の変形が一意に決定できない多自由度メカニズムである場合も多く、変形を一意に定めるために、追加の条件として外力との釣り合いなどの力学的条件を考慮する場合がある。折線が回転剛性をもたないとき、剛体折紙は外力に抵抗できないため、力学的条件を考慮する際には表1の2行目のように剛な面と回転剛性をもつ折線を考慮した機構学的解析と力学的解析の中間的な解析が行われる。
面の変形も許容し、折線に回転剛性を与えた最も実構造物に近い条件での力学、機械学的解析(表1の3行目)も剛体折紙を現実の構造物へ応用するために重要である。この解析ではBarand hingeモデル[27]とよばれるトラスモデルを発展させたトラス部材と回転ばねで構成されるモデルが用いられる。面の面内剛性はトラス部材の軸剛性で、面の面外剛性と折線の回転剛性は回転ばねで表現される。このモデルを応用したウェブブラウザ上で動作するOrigami Simulator[28,29]が公開されており、非常に高速に折り変形を解析可能である。ただし、力学的解析では面の変形を許容しているため、面が剛であるという幾何学的条件に由来した現象の解析には使用できない。さらに、局所的な変形や応力分布などの詳細な解析を行う場合には、図3(c)に示すような面をシェル要素でモデル化した有限要素モデルも使用されるが、計算コストが大きいため大規模なモデルの解析には向いていない。
著者らは表1の2行目の中間的な解析のために図3(d)に示す梁部材を折線部分でヒンジ接合したフレームモデル[30,31,32]および図3(e)に示す剛なパネルを頂点位置でピン接合したPanel-pinモデル[33]を新たに提案している。これらのモデルでは、頂点の支持条件や集中荷重、重力などの外力を単純な定式化で容易に考慮可能であり、かつトラスモデルのように複雑に部材を組むことなく、モデルの構成要素を機械的に配置するだけで面の面内・面外剛性を保証できる。次節ではフレームモデルの定式化を概説する。

フレームモデル
フレームモデル[30,31,32]は図3(d)に示すように梁要素を面上で剛接合、折線上でヒンジ接合したモデルである。4以上の辺をもつ面は三角形分割し、各三角形の重心と辺の中点を接続するように部材を配置する。梁要素を面上で剛接合することで、トラスモデルのように立体的に部材を組むことなく面の剛性を保証できる。フレームモデルの構成要素は剛体折紙の頂点位置には基本的に存在しないが、面が変形しないときフレームモデルの節点座標と剛体折紙の頂点座標は線形方程式で一意に対応付けられるため、容易にフレームモデルの節点座標から折紙の頂点座標を求めることができる。
フレームモデルでは、部分剛接合骨組[34,35]の手法を応用して剛体折紙の変形メカニズムを解析する。フレームモデルでは部材の並進・回転変位と節点の並進・回転変位、ヒンジの初期角からの回転角変化量をそれぞれ独立に扱い、部材端ごとに、その接合条件に応じてこれらの変位の適合条件を定式化する。まず、部材端が剛接合の場合の適合条件を定式化する。フレームモデルの部材数、節点数をそれぞれNM,NNとおき、図4に示すように、部材i(=1,…,NM)の中央点の並進変位と回転変位をそれぞれVi,Ψi∈R3、節点k(=1,…,NN)の並進変位と回転変位をそれぞれUk,Θk∈R3とする。部材iのj端(j=1,2)が節点kに接続するとき、部材端と節点の並進変位が等しいことから、初期状態において部材iの中央点からj端に向かうベクトルをdi,j∈R3として、部材中央点と節点の変位は次式を満たす必要がある。
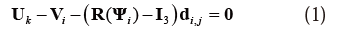
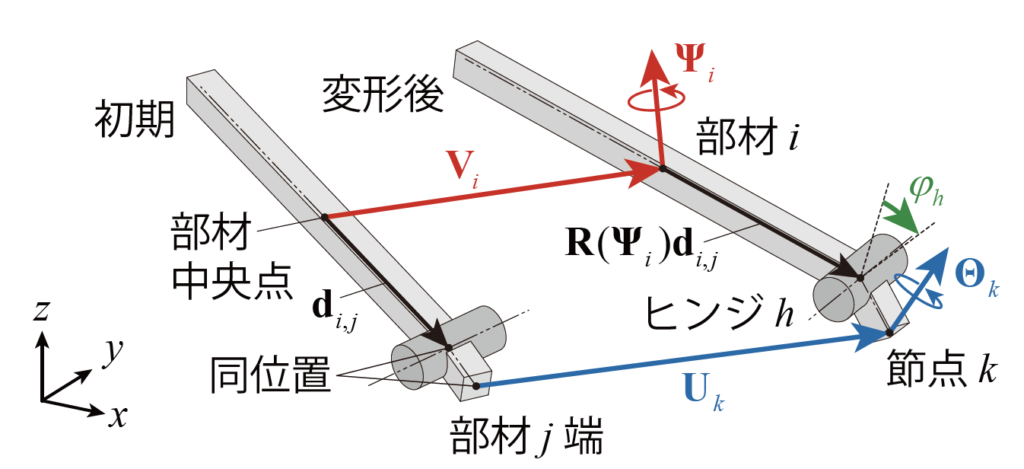
ここで、R(Ψi)∈R3×3は回転ベクトル Ψiに関する回転行列[36]、I3∈R3×3は単位行列である。また、部材iのj端が節点kで剛接合されるとき、部材iと節点kの回転変位が等しいことから、部材中央点と節点の変位は次式を満たす必要がある

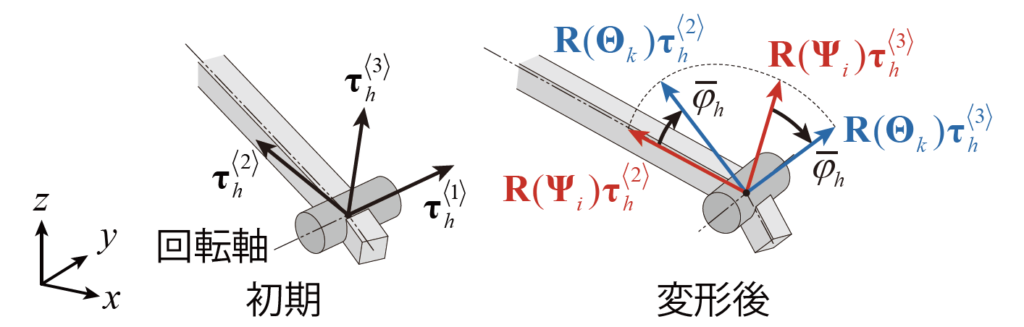
次に、部材iのj端が節点kでヒンジ接合される場合の変位の適合条件式を示す。ヒンジ接合の場合も、部材端と節点の並進変位に関する適合条件式は式(1) で表される。一方、ヒンジの回転軸に沿った相対回転が許容されるため、回転変位に関する適合条件式は式(2) とは異なる。フレームモデルのヒンジ数をNHとおき、図5に示すように初期状態においてヒンジh(=1,…,NH)の回転軸に沿った単位ベクトルをτh<1>∈R3とする。さらに、τh<2>,τh<3>∈R3 を次式を満たす単位ベクトルとして与える。
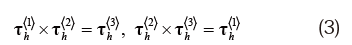
これらのτh<1> 、τh<2>、τh<3>を用いてヒンジの姿勢を表す「枠」(局所座標系)を定義する。部材iのj端が節点kでヒンジhによりヒンジ接合されるとき、τh<2>、τh<3>を節点 とともに回転させたベクトルが τh<1>を部材iと共に回転させたベクトルと直交することから、部材中央点および節点の変位は次式を満たす必要がある。
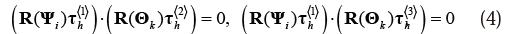
式(4) が満たされているとき、ヒンジ の変位前後の回転角変化量は図5に示すようにR(ψi)τh<2>とR(θk)τh<2> 、またはR(ψi)τh<3>とR(θk)τh<3> のなす角φh である。したがって、独立変数として扱うヒンジhの変位前後の回転角変化量をφh ∈Rとすると、 φhおよび部材中央点と節点の変位は次式を満たす。
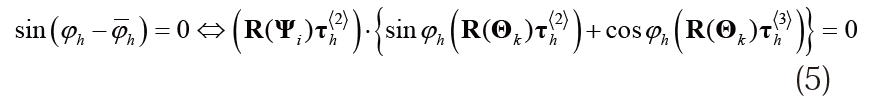
非拘束部材中央点変位Vi,Φi非拘束節点変位Uk,θkおよびヒンジ回転角変化量Φhを全部材、節点、ヒンジに関してまとめた一般化変位ベクトルをX∈RNXとおく。ここで、
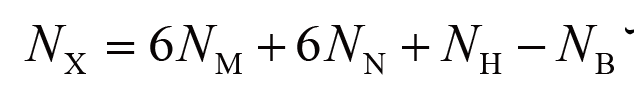
であり、NBは拘束変位自由度数である。このとき,式(1)、(2)、 (4)、 (5) の左辺を全部材端に関し
てまとめたベクトルを Xの関数としてG(X)∈RNG とおく。ここで、NG=12NM であり、G(X)は非適合量ベクトルと呼ばれる。G(X)を用いてフレームモデル全体の一般化変位Xに関する適合条件式は以下のように書ける。

モデルの支持条件は部材または節点変位のうち拘束されている成分を一般化変位ベクトルに含めないことで考慮されている。したがって、図3(d) のように面の重心と辺の中点のみに節点が配置されている場合には頂点の変位を拘束することができない。頂点変位を拘束する場合には、文献[32] に示すように頂点に新たに配置した節点と面または辺上の節点をそれぞれ剛接合するように追加の部材を配置する。
剛体折紙の変形メカニズム解析
剛体折紙の変形メカニズム解析は、式(6) を満たす一般化変位を求めることに他ならない。モデルが剛体折り可能であるとき、これらの適合条件式の解は一意に定まらず、いくつかのパラメータを用いて解が表現される。このパラメータの数は変形自由度(DOF)とよばれ、変形自由度が1のものを1自由度メカニズム、2以上のものを多自由度メカニズムとよぶ。剛体折紙における1自由度メカニズムの代表例にミウラ折りがある。適合条件式は非線形方程式であり、解を数式で解析的に求めることは困難である。そこで、適合条件式をテイラー展開し、高次項を無視した微小変形メカニズム解析が行われる[35]。1階微分の項までを考慮した場合の解は1次の微小変形メカニズムとよばれる。このとき、適合条件式は線形方程式となり容易に解くことが可能であることから、1次の微小変形メカニズムは剛体折紙の変形メカニズムの解析や剛体折り過程の追跡に広く用いられている。非適合量ベクトルG(X)∈RNG の第i成分を Gi(X)(i=1,…,NG)、一般化変位ベクトルX∈RXの第j成分を Xj(j=1,…,NX)とし、(i,j) 成分が∂ Gi(X0)/∂ Xjである行列を Γ0∈RNG×NXとおくとき、次式を満たすベクトル X’∈RNXをX=X0における1次の微小変形メカニズムとよぶ。

式(7) を満たす X’の導出方法は文献[30, 34, 35] 等を参照すること。フレームモデルの場合、一般化変位ベクトルX は部材中央点と節点の変位およびヒンジの回転角変化量で構成されていることから、1次の微小変形メカニズムにおける微小変位増分 Vi‘、Ψi‘、Uk‘、θk‘およびφh‘を式(7) より求めることができる。
多自由度メカニズムの場合、剛体折りによる変形経路を定めるパラメータが複数存在するため、経路が無数に存在する。数値解析により変形経路を追跡する場合、無数に存在する経路のうち一つを選択して追跡する必要があるため、何かしらの経路選択基準を導入する必要がある。筆者らは、経路選択の基準として力の釣り合いに着目し、節点荷重や重力下での剛体折り経路の追跡手法を提案している[32, 33]。提案手法では、モデルの全ポテンシャルエネルギーを変位の適合条件式のもとで最小化し、外力との釣合形状を求めている。力の釣り合いを考慮したとき、多くの折り状態で変形経路はエネルギーを最小化する方向に一意に定まる。しかし、完全に平面展開された平坦状態では変形経路が分岐し、複数の異なる経路が得られることを文献[32, 33] で示している。
参考文献
[22] Y. Zhu, M. Schenk, E. T. Filipov, A review on origami simulations: From kinematics, to mechanics, toward multiphysics, Appl. Mech. Rev., Vol. 74, No. 3, article no. 030801, 2022.8
[23] T. Tachi, Simulation of rigid origami, in Origami4, AK Peters, pp. 175–187, 2009
[24] 渡邉尚彦,剛体折紙モデルの特異状態における可折条件,日本応用数理学会論文誌,Vol. 28, No. 1, pp. 54–71, 2018.3
[25] T. Tachi, Rigid Origami Simulator, http://www.tsg.ne.jp/TT/software/ (Accessed Sept. 2023)
[26] M. Schenk and S.D. Guest, Origami folding: A structural engineering approach, in Origami5, CRC Press, pp. 291–303, 2011
[27] E.T. Filipov, K. Liu, T. Tachi, M. Schenk, and G.H. Paulino, Bar and hinge models for scalable analysis of origami, Int. J. Solids Struct., Vol. 124, pp. 26–45, 2017.10
[28] A. Ghassaei, E.D. Demaine, and N. Gershenfeld, Fast, interactive origami simulation using GPU computation. in Origami7, Tarquin, pp. 1151–1156, 2018
[29] A. Ghassaei, Origami Simulator, https://origamisimulator.org/ (Accessed Sept. 2023)
[30] K. Hayakawa and M. Ohsaki, Form generation of rigid origami for approximation of a curved surface based on mechanical property of partially rigid frames, Int. J. Solids Struct., Vol. 216, pp. 182–199, 2021.5
[31] 早川健太郎,丸山悠斗,安達瑛翔,大崎 純,切り目のある剛体折紙による曲面近似,日本建築学会計画系論文集,Vol. 87, No. 801, pp. 2288–2297, 2022.11
[32] K. Hayakawa and M. Ohsaki, Equilibrium path and stability analysis of rigid origami using energy minimization of frame model, Front. Built Environ., Vol. 8, 2022.8
[33] K. Hayakawa and M. Ohsaki, Panel-pin model for kinematic and equilibrium analysis of rigid origami, Proc. IASS symposium 2023, pp. 1728-1740, 2023.7
[34] 津田勢太,大崎 純,菊川翔平,寒野善博,部分剛接合骨組の安定性評価とメカニズムの解析,日本建築学会構造系論文集,Vol. 78, No. 686, pp. 791–798, 2013
[35] R. Watada and M. Ohsaki, Series expansion method for determination of order of 3-dimensional bar-joint mechanism with arbitrarily inclined hinges, Int. J. Solids Struct., Vol. 141–142, pp. 78–85, 2018
[36] M. Géradin and A. Cardona, Flexible Multibody Dynamics: A Finite Element Approach, Wiley, 2007