
【高野・大谷研究室】「包む音/取り巻く音」
平面波入射音場の円調和関数展開
修士課程二年生 田中 達宏
はじめに
私は現在、室内音場における反射音の方向分布の分析や音場再現の理論・実装に興味を持ちながら研究に取り組んでいる。「音場」という言葉は、普通我々が体験する3次元空間を音波が伝播している場を指して用いられる。したがって、「室内音場」や「音場再現」もそのような音場を対象としている。しかしながら、新しい研究アイデアについて検討する際、いきなり3次元音場を考えると、問題が複雑になったり計算量が多くなったりして問題の本質を掴み損ねる恐れがある。そのような場合、まずは2次元音場を対象とした検討を行うのが適当である。 そこで本稿は、理論上特に重要である、遠方の波源から原点に向かって平面波が到来する音場、すなわち平面波入射音場について、円調和関数展開による表現を導出する。
極座標系における内部問題の一般解
角周波数 [rad/s]の純音を一定の振幅で発する波源によって励振される2次元平面上の音圧 [Pa]について考える。ただし,波源は原点から十分遠くに位置している(内部問題[1])と仮定する。 音圧に対し,直交座標系における2次元波動方程式
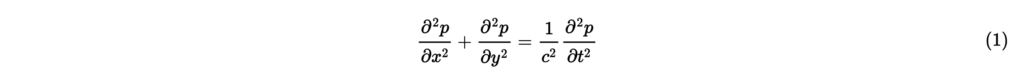
が成り立つ。ただし, [m/s]は音速である。直交座標系におけるラプラシアンと極座標系におけるラプラシアンの関係式
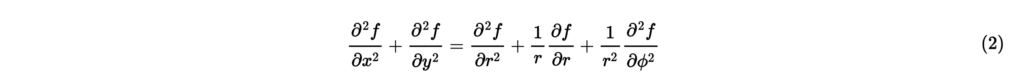
より,極座標系での2次元波動方程式は,
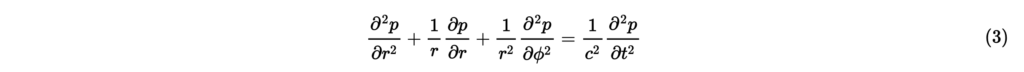
と書ける。ただし,である。図1は直交座標系と極座標系の幾何的関係を示している。

図1 直交座標系と極座標系の幾何的関係。
式(3)で,と変数分離すると,
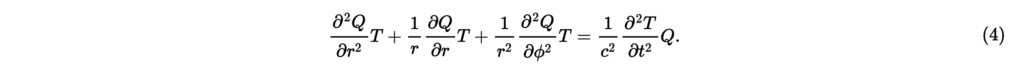
上式の両辺をで割ると,
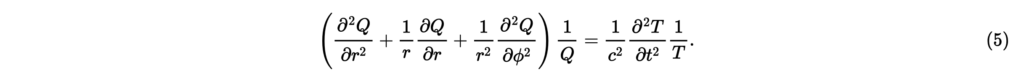
変数とは独立であり,上式の左辺と右辺はそれぞれとのみに依存するため,両辺定数である。 まず時間のみに依存する式(5)の右辺について考える。を定数として,
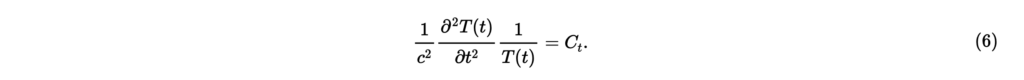
いま角周波数の純音による音場を考えているので,の基本解は,とである。これらの基本解はそれぞれ,ある方向から到来する波・ある方向へと伝播する波に対応する解の時間項となっている。 これらを式(6)に代入すると,
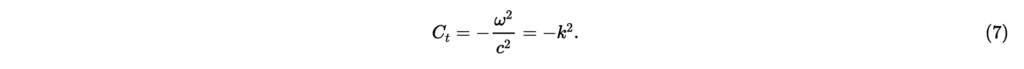
ただし, [rad/m]は波数である。 式(7)を用いて,式(5)は
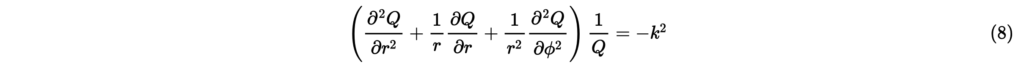
と書き直すことができる。とさらに変数分離すると,
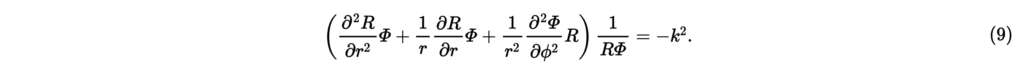
上式の両辺にを掛けて整理すると,
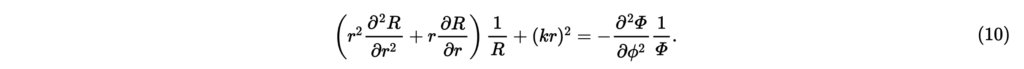
変数とは独立で,上式の左辺と右辺はそれぞれとのみに依存するため,両辺定数である。 偏角ϕのみに依存する式(10)の右辺を考える。を定数として,
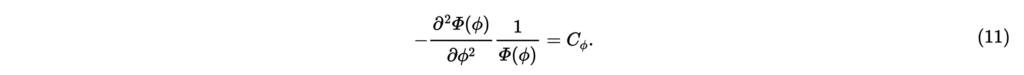
ここで,が成り立つことが必要である。なぜなら,時間と原点からの距離が一定のとき,2次元平面上の音圧は偏角ϕを回転させても不変のはずである。さもなくば,音圧が不連続になってしまう。以上の議論より,nを非負整数として,とを式(11)の基本解として採用する。これらの基本解を式(11)に代入すると,
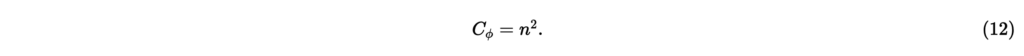
式(12)を用いると,式(9)は,
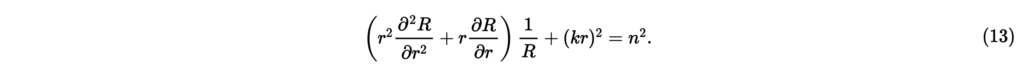
と書き直すことができる。この式の両辺にを掛けて整理すると,
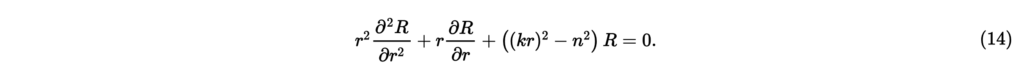
ここで,変数についての関数をとなるように定める。合成関数の微分に注意しながら式(14)のにを代入すると,
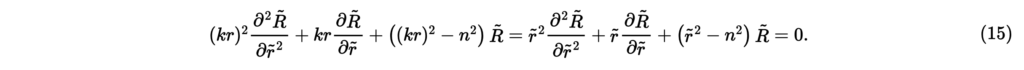
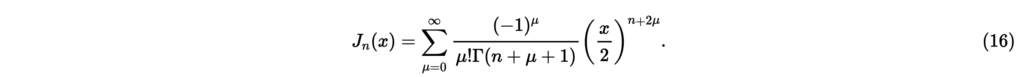
これはベッセルの微分方程式[2]である。が整数の場合の基本解としてベッセル関数とノイマン関数がある。しかしノイマン関数はにおいて無限大となる。したがって,式(15)の基本解としてベッセル関数とJ−n(r~)をここでは採用する。ベッセル関数は次式で定義される[2]。
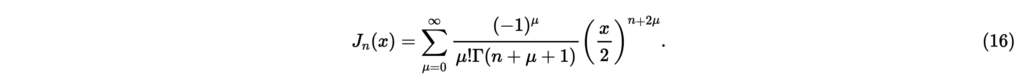
ただし,はガンマ関数で,非負整数に対し!である。ベッセル関数は,整数nについて次の関係が成り立つ[2]。
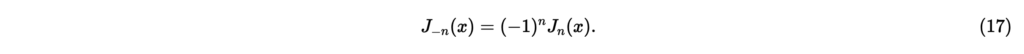
ここまでに導出した基本解を用いて,極座標系における波動方程式の一般解を求めることもできるが,変数ϕに関する解の代わりに円調和関数
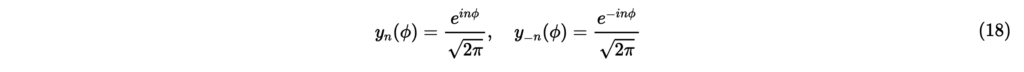
を用いる。円調和関数は,以下のような正規直交性をもつ。
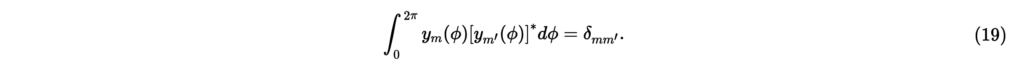
ただし,は複素共役,は整数,はクロネッカーのデルタである。 解として円調和関数をわざわざ用いる理由は,3次元次元波動方程式の球座標系における解(特に球面調和関数)との一貫性を持たせるためである。以上より,極座標系における2次元波動方程式の内部問題の一般解は,
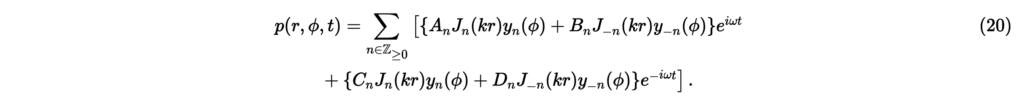
ただし,は非負整数全体の集合,はベッセル関数と円調和関数の次数に依存する任意定数である。次章では,内部問題の中でも特に波源が平面波を発する状況を考え,式(20)の任意定数を具体的に求める。
平面波入射音場の円調和関数展開
原点から十分遠くに位置する波源が一定の振幅で角周波数の平面波を発するとき,原点近傍の平面波入射音場は,ベクトルを用いて
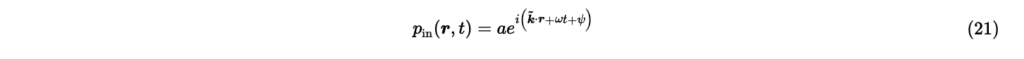
と表される。ただし,は平面波の振幅,[rad]は時刻のときの原点での平面波の位相,rは位置ベクトルである。は波数ベクトルで,は平面波の到来方向を指す単位ベクトルである。これ以降,簡単のためにa=1,とする。 ベクトルで表現された式(21)の解を極座標系での表現に書き改める。すなわち,,として式(21)に代入すると,
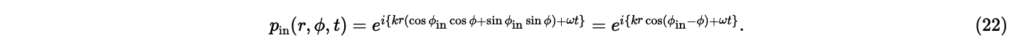
ただし, [rad]は平面波の到来方向である(図2)。

図2 波数ベクトルと平面波の到来方向。
式(20)と式(22)を比較して,任意定数を求める。式(22)にはの項が無いので,である。したがって,
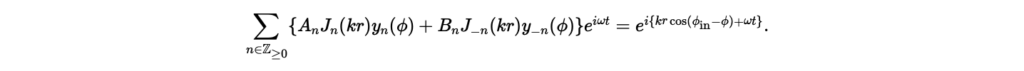
両辺をで割ると,
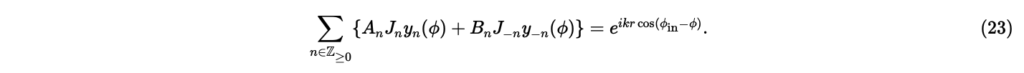
まず,の場合について考える。このとき,であるため,としてだけについて考えれば良い。式(23)の両辺にを掛けて,ϕについて0から2πまで積分すると,円調和関数の正規直交性(19)より,
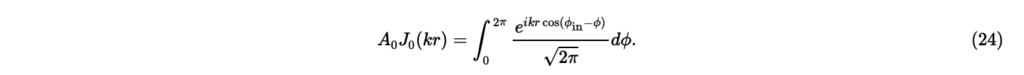
より,式(24)にを代入すると,
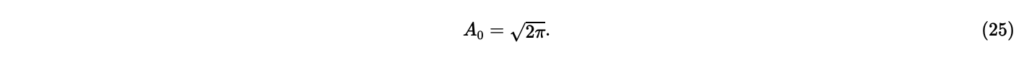
次に,ある正の整数mについての係数Amを考える。式(23)の両辺にを掛けて,式(24)を導いたときと同様の操作をすると,
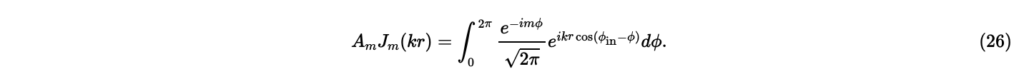
を求めたときと同様にを代入すると,となり,上手くいかない。そこで,両辺をrに関してm階微分してからを代入する。まず左辺について,式(16)より,
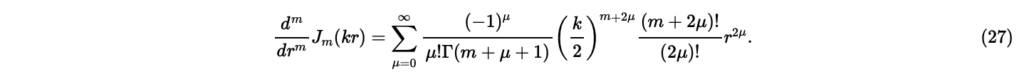
のとき,右辺のμ≠0の項は全てゼロになるので,
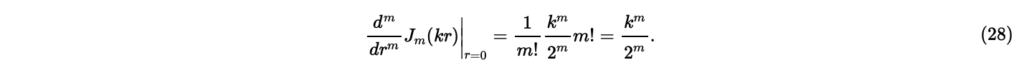
次に式(26)の右辺の被積分関数のrに関するm階微分を,オイラーの公式と二項公式を用いて展開すると,
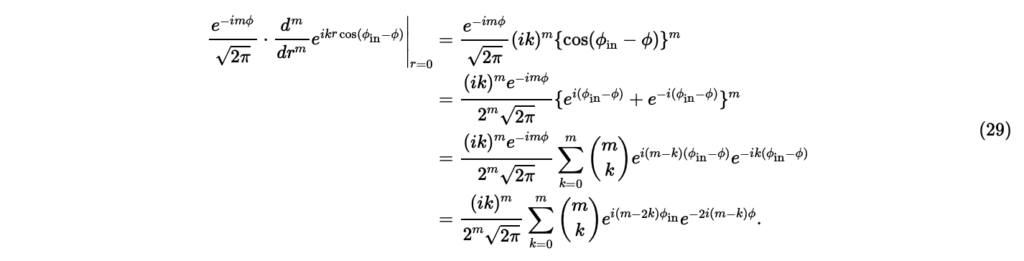
の項は積分するとゼロになるので,
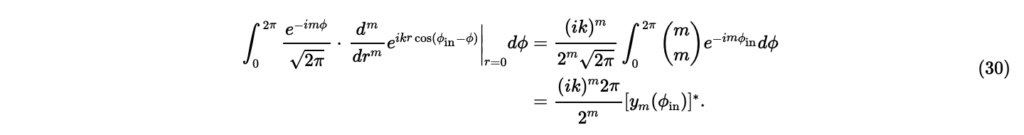
式(26),(28),(30)より,
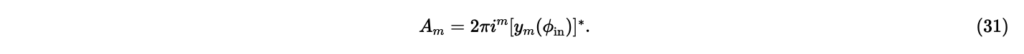
最後に,正の整数mに対する係数を考える。式(23)の両辺にを掛けてから,式(24)を導いたときと同様の操作と式(17)により,
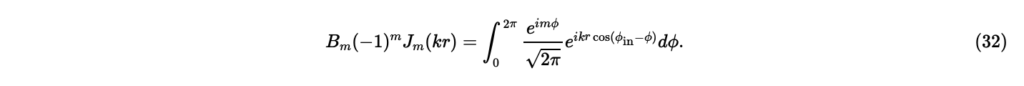
まず左辺についてに関してm階微分する。式(28)の結果を利用することにより,
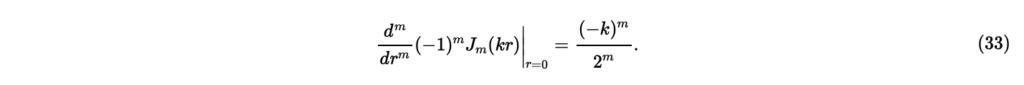
次に式(32)の右辺の被積分関数のrについてのm階微分は,式(29)での計算を利用して,
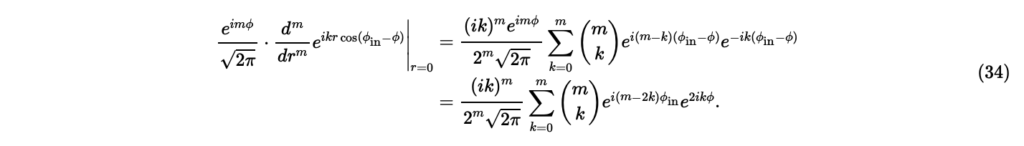
の項は積分するとゼロになるので,
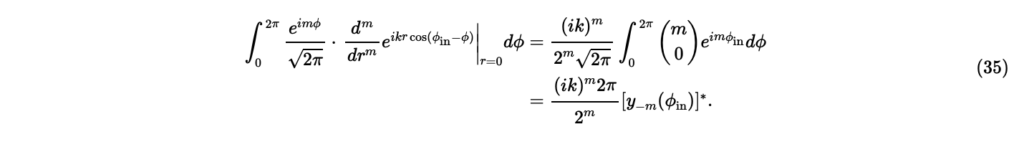
式(32),(33),(35)より,
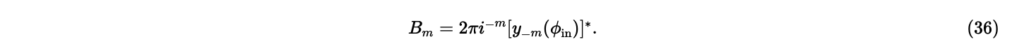
式(23),(25),(31),(36)をまとめると,時間項を除いた平面波入射音場の円調和関数展開は,
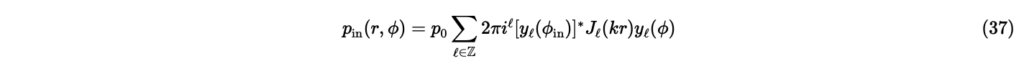
と表される。ただし,Zは整数全体の集合である。は到来平面波の複素振幅で,とはぞれぞれ平面波の振幅と原点での位相を表している。 現実には,式(37)のような整数全体についての和を計算することは不可能であるため,以下のように適当な範囲で無限和を打ち切る必要がある。
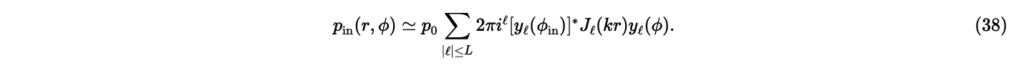
ただし,は絶対値が以下の整数について和をとることを意味する。また,Lを打ち切り次数と呼ぶ。例として,波数,平面波の到来方向,複素振幅,打ち切り次数とした場合のの実数部を図3に示す。

図3
おわりに
本稿は,極座標系における内部問題の一般解と平面波入射音場の円調和関数展開の導出過程を明らかにした。これらの理論は室内音場の分析や音場再現の研究を遂行する上で必須である。本稿の内容がこれらの研究分野に関心のある読者にとって,有益であることを願う。 最後に,私からの質問にメールで丁寧な回答をしていただいた電気通信大学の任逸さん,本稿の掲載に関わって下さった編集委員の皆様に感謝します。
1. E. G. Williams, 吉川茂, 西條献児. フーリエ音響学: 音の放射と近距離場音響ホログラフィの基礎. (シュプリンガー・フェアラーク東京, 東京, 2005) \\ 2. J. Mathews and R. L. Walker. Mathematical methods of physics. (W. A. Benjamin, Inc., New York, 1964)







